Everett's Many Worlds and the "copies of yourself" you will never meet. Or will you?

Every quantum transition that takes place in every distant corner of the universe, fragments our local world into myriads of its copies.

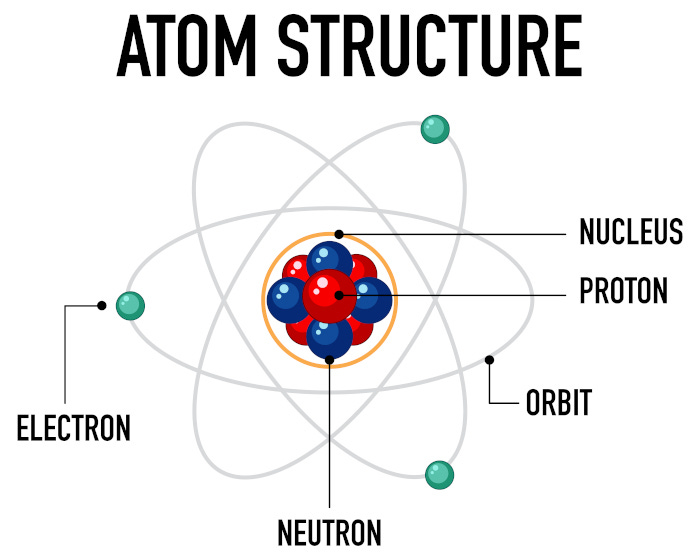
In 1897, J. J. Thomson (1856-1940) discovered the electron. Let’s play a mental game and try to visualize the electron in relation to the atomic nucleus. I bet many of you right now are mentally visualizing the image of a small electron spinning around a nucleus while staying within its orbit. This is the classical model of the atom that Ernest Rutherford (1871-1937; Thomson’s student) gave us in 1909. Models are used to convey information, and what does this model tell us? That the mass of the atom is concentrated almost entirely in the center, in the nucleus, and that its total “area” is completed by the orbits of the electrons that orbit it. Sort of like a miniature solar system. Now, Rutherford did not know quantum mechanics, and the subatomic world was in its infancy, so while it is normal for us to talk about subatomic particles, it was not so easy for physicists in the early twentieth century. Our mental images are much richer in details and particulars, but during the last century people used patterns and models observable in nature or handed down from time to time from the past (the idea that things are composed of atoms comes from ancient Greece).
So this can be called a classic form of the atom, we are familiar with it, and that is why it is generally the first thing we mentally visualize when we talk about atoms.

Classical atom structure model - Freepik

Electrons are the ones who make all the mess

Rutherford did not stop at the surface composition of the atom, he went much further and showed that the nucleus is not elementary because it is itself composed of protons (positively charged) and neutrons (uncharged). Since protons and electrons are equal in value but opposite in charge, an atom with an equal number of the two particles can be said to be electrically neutral and stable. Physicists took another step forward in the 1960s and 1970s when they discovered that protons and neutrons are not elementary particles either, because they are made up of even smaller particles called quarks. We also know that, chemically speaking, electrons are the ones who make all the mess; they are light, snappy, not "still" like atomic nuclei. Electrons are purposeful, flashy, jumpy, like teenagers who cannot sit still at their desks. No sir, they have to move. To me, electrons are “cyberpunk”, which is why I love them.

Particles & Co.

You will be saying, "Michael, you've still got no news, buddy!”
That is true. But bear with me, because I'm getting there. We are now looking at a world of particles, you see? You know those wide angle shots that narrow down to go deeper and deeper into the core of things? We are there, below the surface, in the subatomic world, but now I am going to ask you to resurface, because "reality" is not only made of particles, it is also made of "fields". In classical physics, if a particle has a position in space (and a momentum), then fields are everywhere, occupying all of space. This is why, for example, we can measure the direction in which a magnetic field points, or we can use the tendency of electrons to move when stimulated to measure an electric field; in particular, the greater the acceleration of the electron, the stronger the electric field. So particles and fields.
That's it? Nothing new at all.

The great question

For classical physics this is pretty much it, the basis, in short, but when we enter the world of QM everything (or almost everything) changes. The basic principle here is that reality is not only particles and fields. Electrons are not identified by a position and a momentum, but by a wave function (which we denote by the Greek letter psi Ψ). For quantum physicists, the world is a quantum wave function. We are talking about waves, and therefore probabilities, so where the amplitude of the wave is greater, it is easier to find the particle. In his equation (the fundamental basis of QM), Schrödinger represented the wave associated with the electron. Mathematically, there are an infinite number of solutions to this equation, but only a few are acceptable because they satisfy certain conditions. But let's not go into that, because I want to ask a question: What happens if, instead of leaving everything at the subatomic level, we take it to the level of the whole universe? So what can happen if the whole universe is a single wave function that satisfies the conditions and determinants of the Schrödinger’s equation?

Erwin Schrödinger (here)

Superposition of states

I already have chills! You can stop visualizing small atoms, their nuclei, orbits and all, let's leave classical subatomic model behind for a moment and just use it to explain a concept (no math for now, promise). We know that an electron can have a spin, which is a rotation of the particle around its own axis. There are two possible outcomes to measuring the spin of an electron: spin up and spin down, which coincides with a counterclockwise direction of rotation if the spin is up and clockwise if the spin is down. Now, a measurement, such as a quantum mechanical one, gives us a spin up or spin down result, but whenever we get this result, we do not cancel the other, because the particle does not have predetermined properties (such as position or momentum), but a value that can be determined by the measurement, and therefore the particle is always in a superposition of all possible states (the Heisenberg uncertainty principle). This means that if we express the state of the particle in spin up, we also fix the probability of observing the same particle in spin down.

Where the world splits into many possible worlds

You will say, “Michael, what on earth are you talking about?”
In a quantum system, an electron is identified by a wave function (not an orbit), and this wave function is given by the superposition of the different possible states of the electron. From this principle we arrive at one of the most fascinating theories in quantum physics: Hugh Everett's Many-Worlds Theory. Everett (1930-1982) was always fascinated by the problem of making measurements in a quantum system. He posed a question: If the entire universe is described by a single wave function, and if that wave function evolves according to Schrödinger's equation, what should the measurement consist of? Well, he came to the conclusion that it is not necessary to measure, because in a quantum system things interact with each other all the time. A quantum system and the measurer are in entanglement, that is, the state of the system at the time of the observation evolves into a superposition of possible results. The measurement of a spin is relative only to the entanglement between the electron and the observer, but all other possible states of the measurement continue to coexist, and to be present they must have a "place" (or quantum system) in which to exist. Simply put, for Everett, all possible results contained in a wave function are actualized, but each in a different copy of the universe, isolated from the others and completely self-sufficient.

Every quantum transition that takes place on every star, in every galaxy, in every distant corner of the universe, fragments our local world into myriads of its copies.
(DeWitt's interpretation of Everett's idea).

Parallel worlds

Thus, according to Everett, there is not a collapse of the wave function at the moment of measurement, so that all other results are canceled out and nullified, but a “multiverse” consisting of all possible results. Therefore, every time an observer makes a measurement, reality splits, creating a parallel world in which a copy of him makes the same measurement and gets a different one of the possible results. Perhaps there is a copy of me writing the same article in another universe, perhaps he has a different view from mine, perhaps in his universe measurements in quantum systems have produced different results and have not yet succeeded in proving the reality of the entangled state.
We will never know, because Everett's theory also predicts that there is total lack of communication between the different universes created by the gaps. In short, we cannot prove it yet, but the idea is really fascinating.

Parallel Worlds - AI generated by DdCode

Let’s talk around it

In this brief overview, I have not described other elements of Everett's theory, implications, or convolutions. I have not mentioned the role of decoherence or the interference, or even probability and statistics. I do not know if I have succeeded in giving an idea of the matter, certainly not a complete one, but I hope it will intrigue you as much as it has intrigued me. Meanwhile, I continue to study. If you know more and want to share, I would love it!

---

More insights

The Many-Worlds Interpretation of Quantum Mechanics: A Fundamental Exposition by Hugh Everett, III, With Papers by J. A. Wheeler, B. S. Dewitt, L. N. Cooper and D. Van Vechten, and N. Graham Bryce Seligman Dewitt. Princeton University Press; (2015).

The Emergent Multiverse: Quantum Theory According To The Everett Interpretation, David Wallace. Oxford University Press; (2014).

Something Deeply Hidden: Quantum Worlds and the Emergence of Spacetime, Sean Carroll. Oneworld Publications (2019).

---